Cachemiss

Parallel reduce and scan on the GPU

Introduction

GPUs are formidable parallel machines, capable of running thousands of threads simultaniously. They are excellent for embarassily parallel algorithms, but are quite different than the ones on the CPU due to the way GPUs work. You can’t just build and run an application. You need to interact with the GPU driver via one of several APIs available (CUDA, OpenCL, Vulkan, DirectX, OpenGL, etc), manage the device memory, organize the transfers between the host and the device, and dispatch the shaders that will run on the GPU.

We’ll have a look at two basic algorithms: reduce and scan. They are basic building blocks for more complex algorithms, e.g. solving linear equations or stream compaction. We’ll use Vulkan with GLSL shaders compiled to SPIR-V and its subgroup features introduced in version 1.1. This is chosen as it runs on many GPUs (NVidia, Intel, AMD, Mali, etc) and run on multiple platforms (Windows, Linux, Android, etc). It makes it easier to use than, say, CUDA.

To understand what a subgroup is, let’s review the abstract model used by Vulkan. Vulkan dispatches a certain number of shaders, which are divided in a number of work groups, themselves in a number of subgroups, and each one is divided in a number of invocations.

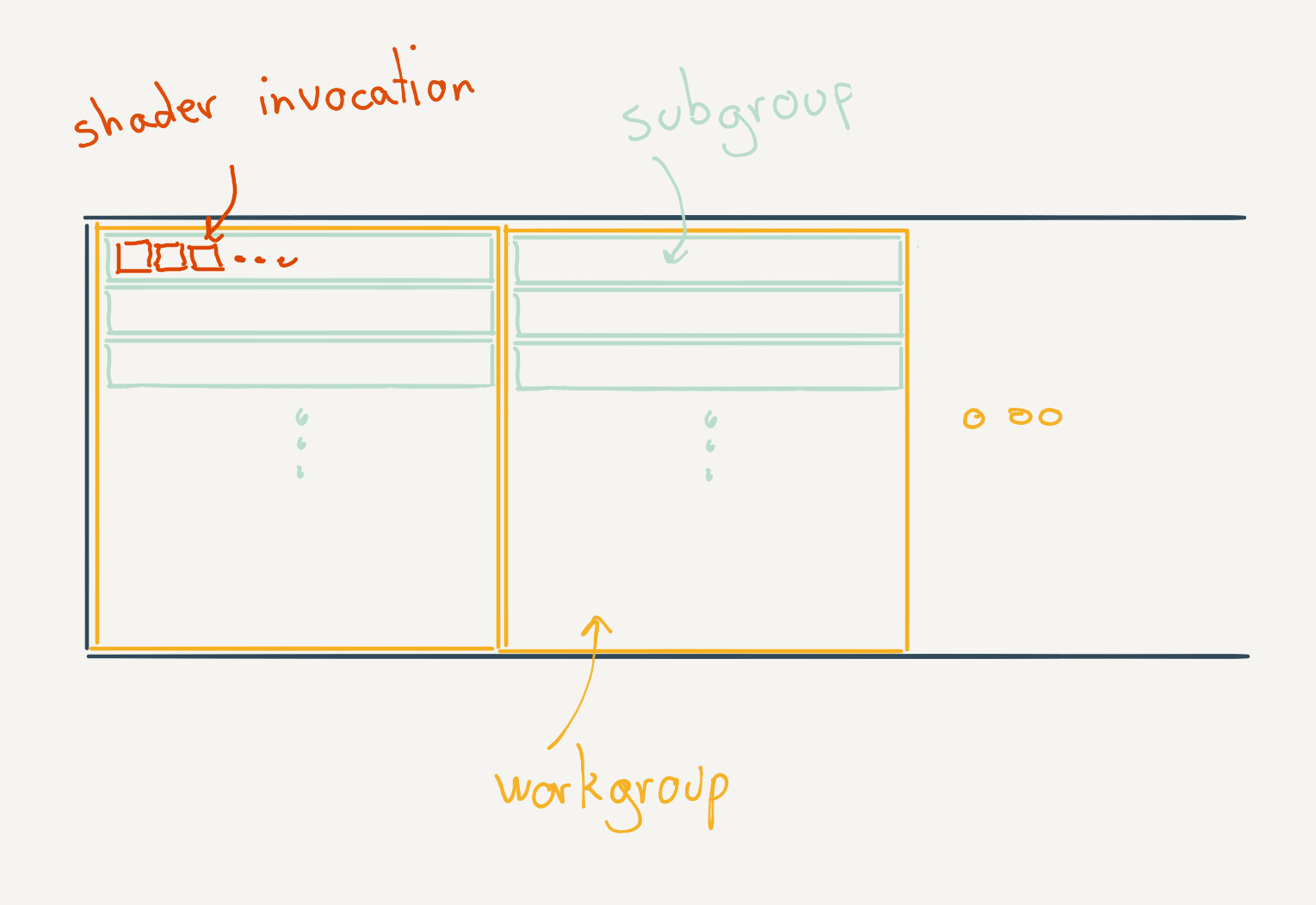
Each work group has its own cache that can be accessed directly by the shaders, called shared memory. Obviously accessing this memory is much faster than the global memory and algorithms are designed to make as much us of it as possible. The next subdivision, workgroups, are essentially large SIMD groups that execute the invocations in lockstep. Each SIMD, or subgroup, can communicate with special instructions, bypassing the shared memory or global memory.

Vulkan subgroups

Vulkan mandates some minimum requirements for subgroups for all drivers supporting version 1.1 We can query those capabilities to get information such as the size of subgroups (i.e. how many shaders run per subgroup) and which operations are supported.

auto properties = 
  physicalDevice.getProperties2<vk::PhysicalDeviceProperties2, vk::PhysicalDeviceSubgroupProperties>();
auto subgroupProperties = 
  properties.get<vk::PhysicalDeviceSubgroupProperties>();

std::cout << "Subgroup size: " 
          << subgroupProperties.subgroupSize 
          << std::endl;

std::cout << "Subgroup supported operations: " 
          << vk::to_string(subgroupProperties.supportedOperations) 
          << std::endl;

On my machine with a Vega 56, the following is returned:

Subgroup size: 64
Subgroup supported operations: {Basic | Vote | Arithmetic | Ballot | Shuffle | ShuffleRelative | Quad}

Arithmetic is the type of operation we’ll need to implement scan and reduce. An introduction to the other operations can be found at this tutorial khronos vulkan subgroup

Reduce

Reduce is very simple, it takes a list of elements \(x_0, x_1, x_2, ...\) and calculates its sum,

C++17 has added it as std::reduce which can be run in parallel or sequentially. We’ll use it to compare the performance with the one running on the GPU. The equivalent operation in Vulkan for subgroups is:

float sum = subgroupAdd(value);

Every invocation belonging to the subgroup will return the total sum.

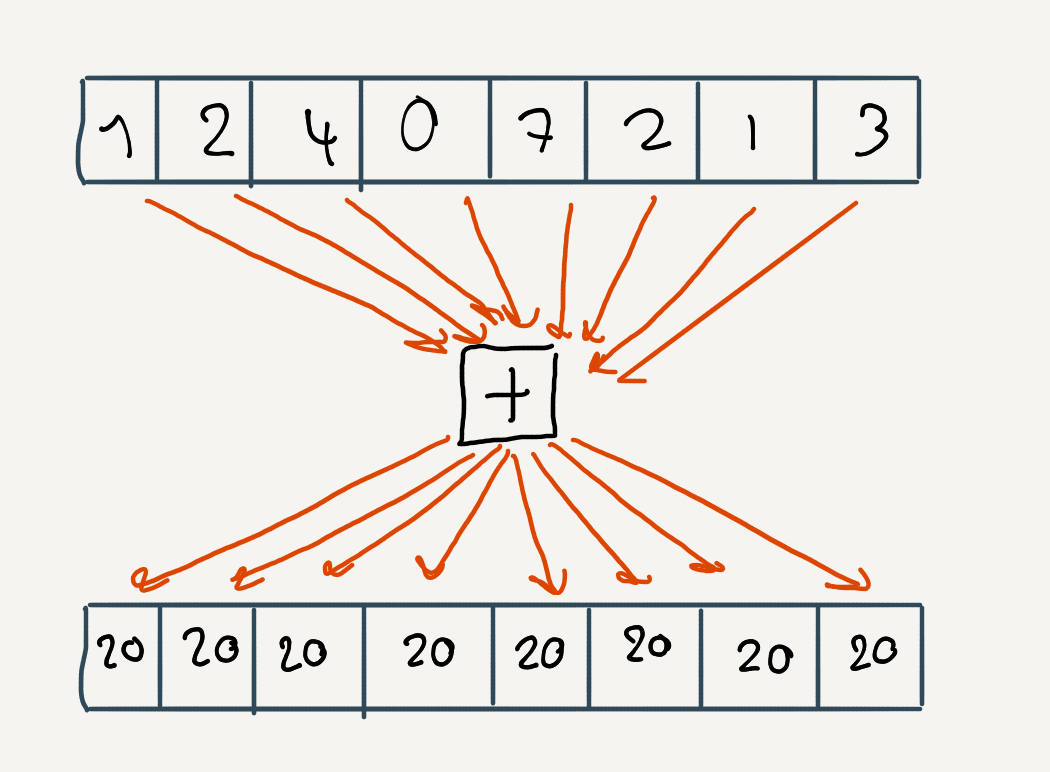
We can reduce up to 64 values on my machine. We’ll want to reduce on more elements than that, so we can use multiple subgroups to each reduce a part of the list of elements. We’ll then need to save the sum of each subgroup in the shared memory. Assuming we have less number of subgroups then the size of a subgroup, we load those values from the shared memory in the first subgroup and call subgroupAdd again. We choose then one invocation to save the sum in global memory.

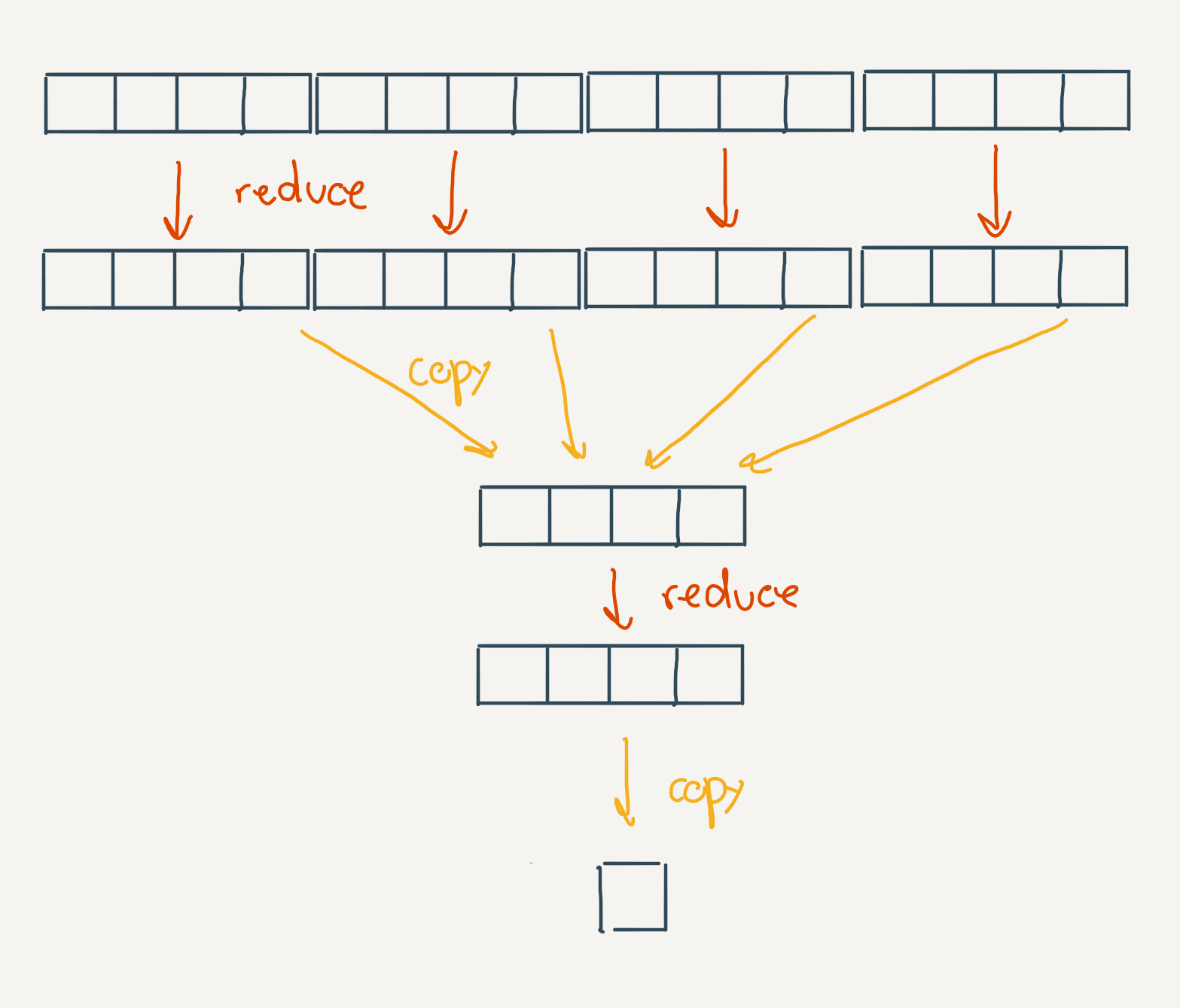
Note that we’re still limited to the maximum size of a work group. Since workgroups can’t be synchronized between each other, we’ll need to use atomicAdd or simply run the entire algorith in multiple passes. This allows us to insert a barrier between the passes to synchronize the global memory on the device. At the end of the first pass, we’ll have N number of elements summed, corresponding to N workgroups, we then insert a memory barrier and dispatch again N invocations which will sum the elements with the same shader.

The reduce shader then looks like this (omitting details about declaring the input, output, sizes, etc),

shared float sdata[sumSubGroupSize];

void main()
{
  float sum = 0.0;
  if (gl_GlobalInvocationID.x < consts.n)
  {
    sum = inputs[gl_GlobalInvocationID.x];
  }

  sum = subgroupAdd(sum);

  if (gl_SubgroupInvocationID == 0)
  {
    sdata[gl_SubgroupID] = sum;
  }

  memoryBarrierShared();
  barrier();

  if (gl_SubgroupID == 0)
  {
    sum = gl_SubgroupInvocationID < gl_NumSubgroups ? 
      sdata[gl_SubgroupInvocationID] : 0;
    sum = subgroupAdd(sum);
  }

  if (gl_LocalInvocationID.x == 0)
  {
    outputs[gl_WorkGroupID.x] = sum;
  }
}

Let’s see how fast this algorithm is, comparing it with std::reduce running in sequence and in parallel. We’re also comparing with a regular reduce algorithm using only shared memory, based on the excellent slides from Mark Harris: Optimizing parallel reduce in CUDA

That’s rather disapointing, the subgroup based reduce is only slightly faster. However it is much easier to implement than the shared memory based one, and easier to read.

Scan

Scan, or prefix sum, takes a list of elements \(x_0, x_1, x_2, ...\) and produces a sequence of elements \(y_0, y_1, y_2, ...\) such that,

Again, this is available in C++17 with std::inclusive_scan, which we’ll use to compare with the GPU equivalent one. The vulkan subgroup operation is,

float value = subgroupInclusiveAdd(value);

Similarily to reduce, each invocation in the subgroup will receive the partial sum corresponding to its index (in increasing order).

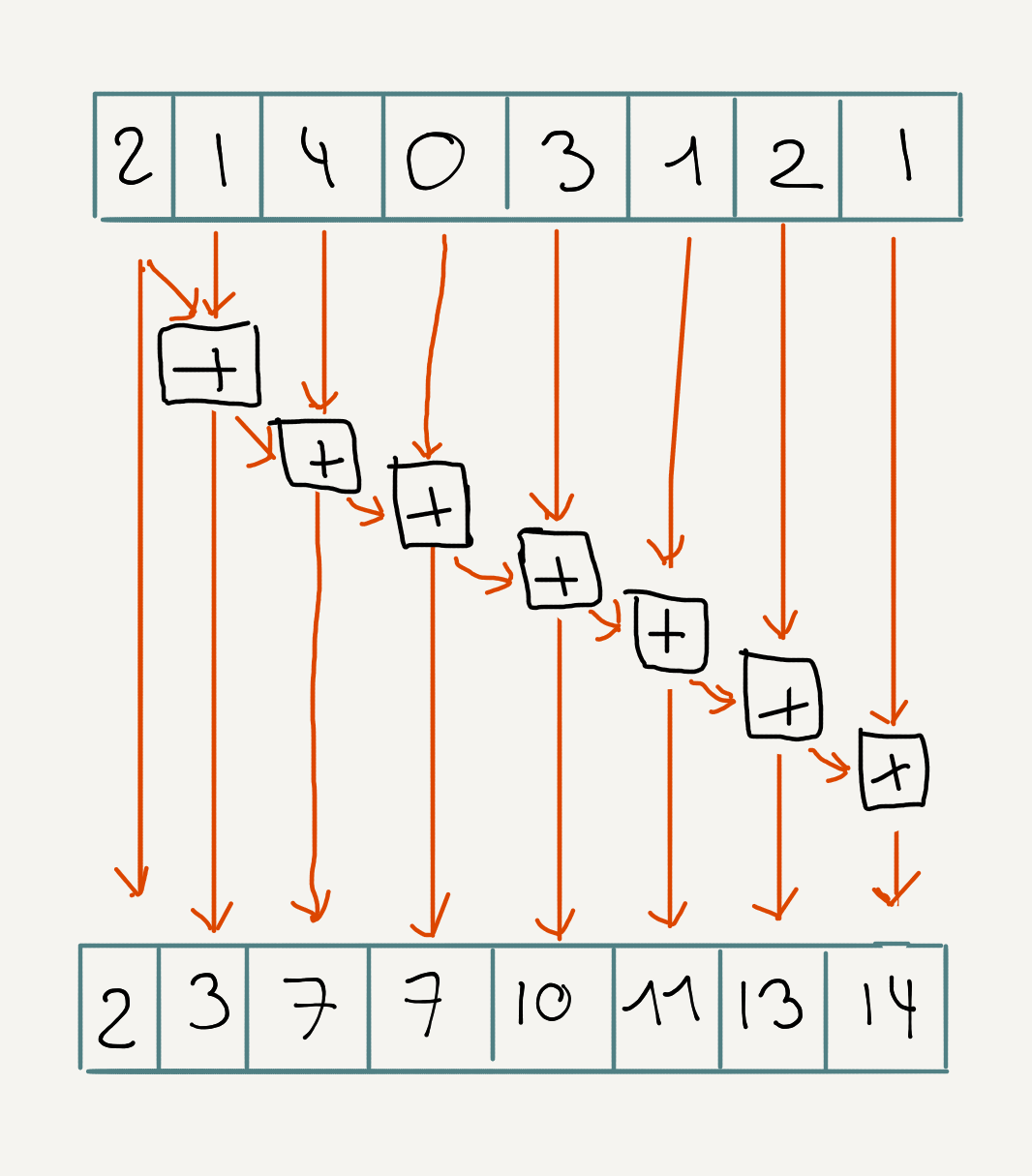
We’ll use a similar strategy as for reduce to be able to scan over a bigger number of elements than the subgroup size. Each subgroup calculates the partial scan, we save the last element of the subgroup (i.e. the total sum of the subgroup) in shared memory. Assuming we have less number of subgroups then the size of a subgroup, we load those values from the shared memory in the first subgroup and call subgroupInclusiveAdd again. Finally we take each element of this subgroup, and add it to the subgroup corresponding to its index (except the first subgroup).

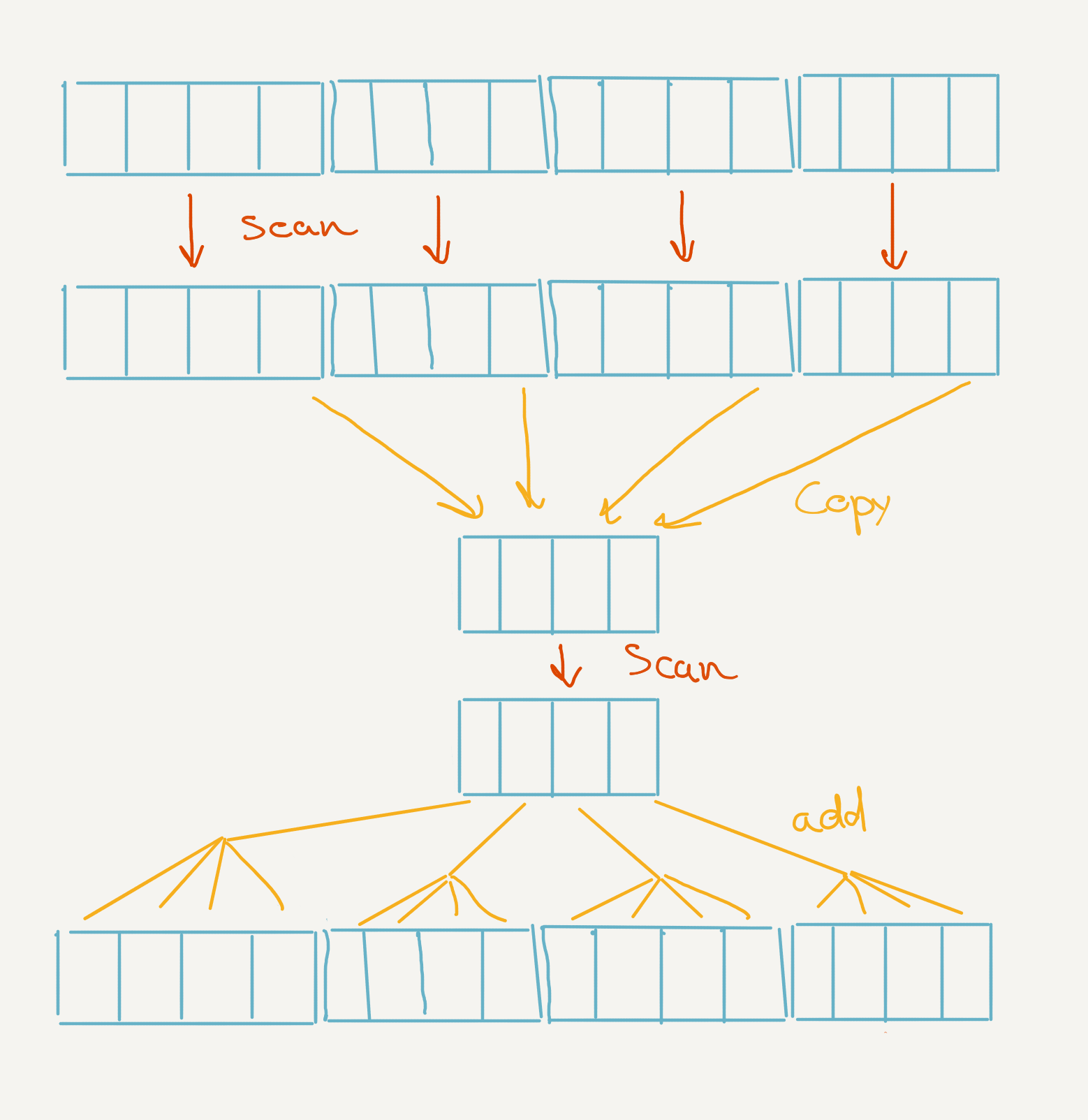
This works because the scan at each subgroup is the scan of the subgroup plus the total sum of every element before. If we look at the equation above and assume a subgroup size of 2, we can look at the calculation as so,

which corresponds to the algorithm described.

Again as with reduce, this limits us to the maximum size of a work group. To go beyond, we’ll also need to do multiple passes. In the first pass, we’ll add the partial scan to the input data and also save it in an intermediate elements. We then perform another scan on the intermediate elements. Finally we need to add the those intermediate elements back to the original elements. Note that those two passes with the intermediate result are essentially the same operations as the ones in the shader.

The scan shader then looks like this (again, omitting declaration for inputs, sizes, etc),

shared float sdata[sumSubGroupSize];

void main()
{
  float sum = 0.0;
  if (gl_GlobalInvocationID.x < consts.n)
  {
    sum = inputs[gl_GlobalInvocationID.x];
  }

  sum = subgroupInclusiveAdd(sum);

  if (gl_SubgroupInvocationID == gl_SubgroupSize - 1)
  {
    sdata[gl_SubgroupID] = sum;
  }

  memoryBarrierShared();
  barrier();

  if (gl_SubgroupID == 0)
  {
    float warpSum = gl_SubgroupInvocationID < gl_NumSubgroups ? sdata[gl_SubgroupInvocationID] : 0;
    warpSum = subgroupInclusiveAdd(warpSum);
    sdata[gl_SubgroupInvocationID] = warpSum;
  }

  memoryBarrierShared();
  barrier();

  float blockSum = 0;
  if (gl_SubgroupID > 0)
  {
    blockSum = sdata[gl_SubgroupID - 1];
  }

  sum += blockSum;

  if (gl_GlobalInvocationID.x < consts.n)
  {
    outputs[gl_GlobalInvocationID.x] = sum;
  }

  if (gl_LocalInvocationID.x == gl_WorkGroupSize.x - 1)
  {
    partial_sums[gl_WorkGroupID.x] = sum;
  }
}

The shader to add the partial scan back to the list of elements is,

shared float sum;

void main()
{
  if (gl_WorkGroupID.x > 0 &&
      gl_GlobalInvocationID.x < consts.n)
  {
    sum = 0.0;
    if (gl_LocalInvocationID.x == 0)
    {
      sum = i.value[gl_WorkGroupID.x - 1];
    }

    memoryBarrierShared();
    barrier();

    o.value[gl_GlobalInvocationID.x] += sum;
  }
}

Again, let’s see how this fares against a CPU implementation and a GPU implementation using shared memory only. We’ve used the implementation from GPU Gems 3.

This is very impressive, much better improvements than with the reduce with subgroups!

Github

The implementation of those shaders with Vulkan and the benchmarks can be found on my github. Note that it uses a basic Vulkan engine I wrote, Vortex2D. This is used to implement a 2D fluid engine where the reduce operation is used in a linear solver and the scan operation to remove unused particles.